41.10. Pretraining on Unlabeled Data

from importlib.metadata import version

pkgs = ["matplotlib", 
        "numpy", 
        "tiktoken", 
        "torch",
        "tensorflow" # For OpenAI's pretrained weights
       ]
for p in pkgs:
    print(f"{p} version: {version(p)}")

matplotlib version: 3.8.2
numpy version: 1.26.0
tiktoken version: 0.5.1
torch version: 2.2.2
tensorflow version: 2.15.0

In this chapter, we implement the training loop and code for basic model evaluation to pretrain an LLM At the end of this chapter, we also load openly available pretrained weights from OpenAI into our model

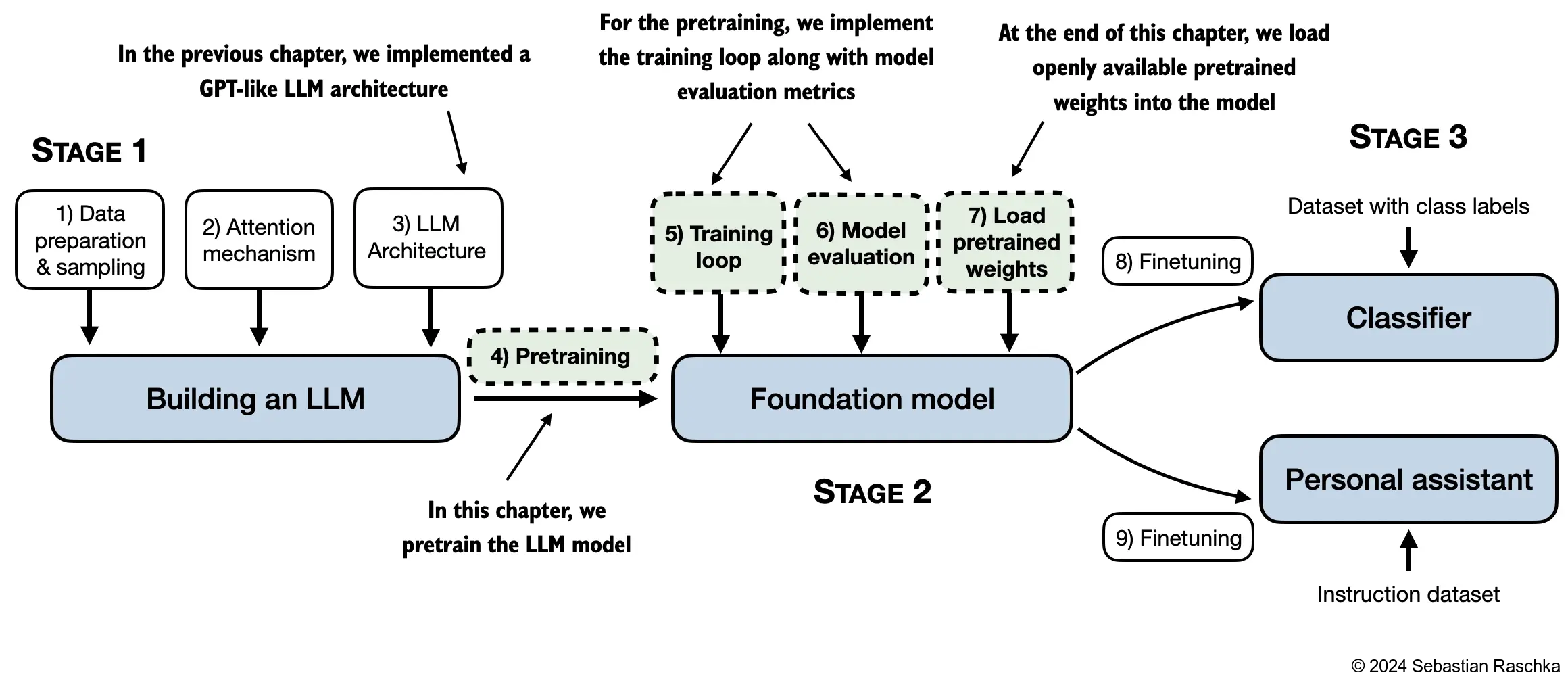
The topics covered in this chapter are shown below

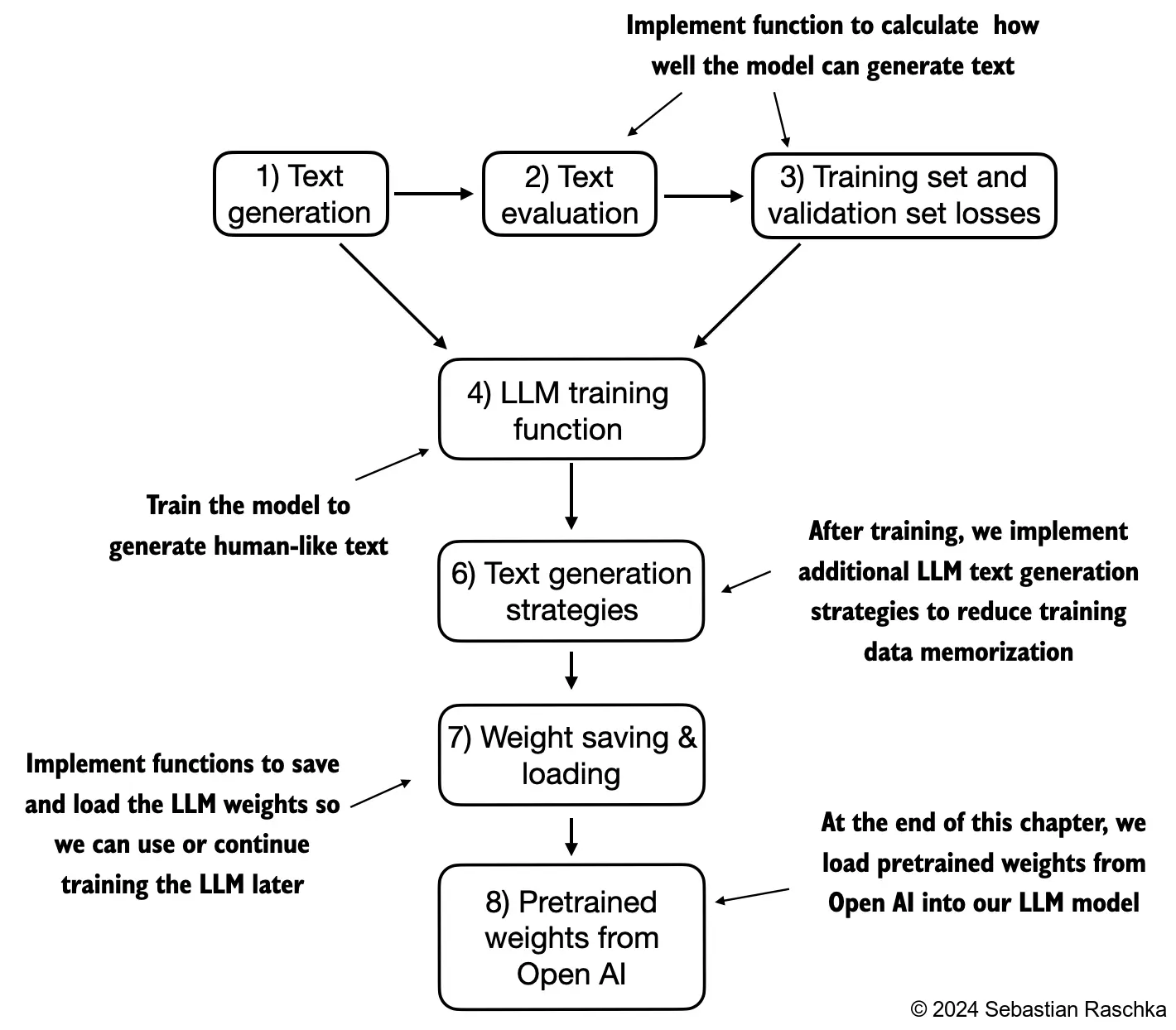
41.10.1. Evaluating generative text models

We start this section with a brief recap of initializing a GPT model using the code from the previous chapter Then, we discuss basic evaluation metrics for LLMs Lastly, in this section, we apply these evaluation metrics to a training and validation dataset

41.10.1.1. Using GPT to generate text

We initialize a GPT model using the code from the previous chapter

#Some relevant codes

import tiktoken
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader

class GPTDatasetV1(Dataset):
    def __init__(self, txt, tokenizer, max_length, stride):
        self.tokenizer = tokenizer
        self.input_ids = []
        self.target_ids = []

        # Tokenize the entire text
        token_ids = tokenizer.encode(txt)

        # Use a sliding window to chunk the book into overlapping sequences of max_length
        for i in range(0, len(token_ids) - max_length, stride):
            input_chunk = token_ids[i:i + max_length]
            target_chunk = token_ids[i + 1: i + max_length + 1]
            self.input_ids.append(torch.tensor(input_chunk))
            self.target_ids.append(torch.tensor(target_chunk))

    def __len__(self):
        return len(self.input_ids)

    def __getitem__(self, idx):
        return self.input_ids[idx], self.target_ids[idx]


def create_dataloader_v1(txt, batch_size=4, max_length=256,
                         stride=128, shuffle=True, drop_last=True):
    # Initialize the tokenizer
    tokenizer = tiktoken.get_encoding("gpt2")

    # Create dataset
    dataset = GPTDatasetV1(txt, tokenizer, max_length, stride)

    # Create dataloader
    dataloader = DataLoader(
        dataset, batch_size=batch_size, shuffle=shuffle, drop_last=drop_last)

    return dataloader

class MultiHeadAttention(nn.Module):
    def __init__(self, d_in, d_out, block_size, dropout, num_heads, qkv_bias=False):
        super().__init__()
        assert d_out % num_heads == 0, "d_out must be divisible by n_heads"

        self.d_out = d_out
        self.num_heads = num_heads
        self.head_dim = d_out // num_heads  # Reduce the projection dim to match desired output dim

        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.out_proj = nn.Linear(d_out, d_out)  # Linear layer to combine head outputs
        self.dropout = nn.Dropout(dropout)
        self.register_buffer('mask', torch.triu(torch.ones(block_size, block_size), diagonal=1))

    def forward(self, x):
        b, num_tokens, d_in = x.shape

        keys = self.W_key(x)  # Shape: (b, num_tokens, d_out)
        queries = self.W_query(x)
        values = self.W_value(x)

        # We implicitly split the matrix by adding a `num_heads` dimension
        # Unroll last dim: (b, num_tokens, d_out) -> (b, num_tokens, num_heads, head_dim)
        keys = keys.view(b, num_tokens, self.num_heads, self.head_dim)
        values = values.view(b, num_tokens, self.num_heads, self.head_dim)
        queries = queries.view(b, num_tokens, self.num_heads, self.head_dim)

        # Transpose: (b, num_tokens, num_heads, head_dim) -> (b, num_heads, num_tokens, head_dim)
        keys = keys.transpose(1, 2)
        queries = queries.transpose(1, 2)
        values = values.transpose(1, 2)

        # Compute scaled dot-product attention (aka self-attention) with a causal mask
        attn_scores = queries @ keys.transpose(2, 3)  # Dot product for each head

        # Original mask truncated to the number of tokens and converted to boolean
        mask_bool = self.mask.bool()[:num_tokens, :num_tokens]

        # Use the mask to fill attention scores
        attn_scores.masked_fill_(mask_bool, -torch.inf)

        attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)
        attn_weights = self.dropout(attn_weights)

        # Shape: (b, num_tokens, num_heads, head_dim)
        context_vec = (attn_weights @ values).transpose(1, 2)

        # Combine heads, where self.d_out = self.num_heads * self.head_dim
        context_vec = context_vec.reshape(b, num_tokens, self.d_out)
        context_vec = self.out_proj(context_vec)  # optional projection

        return context_vec
      
class LayerNorm(nn.Module):
    def __init__(self, emb_dim):
        super().__init__()
        self.eps = 1e-5
        self.scale = nn.Parameter(torch.ones(emb_dim))
        self.shift = nn.Parameter(torch.zeros(emb_dim))

    def forward(self, x):
        mean = x.mean(dim=-1, keepdim=True)
        var = x.var(dim=-1, keepdim=True, unbiased=False)
        norm_x = (x - mean) / torch.sqrt(var + self.eps)
        return self.scale * norm_x + self.shift


class GELU(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x):
        return 0.5 * x * (1 + torch.tanh(
            torch.sqrt(torch.tensor(2.0 / torch.pi)) *
            (x + 0.044715 * torch.pow(x, 3))
        ))


class FeedForward(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Linear(cfg["emb_dim"], 4 * cfg["emb_dim"]),
            GELU(),
            nn.Linear(4 * cfg["emb_dim"], cfg["emb_dim"]),
            nn.Dropout(cfg["drop_rate"])
        )

    def forward(self, x):
        return self.layers(x)


class TransformerBlock(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.att = MultiHeadAttention(
            d_in=cfg["emb_dim"],
            d_out=cfg["emb_dim"],
            block_size=cfg["ctx_len"],
            num_heads=cfg["n_heads"],
            dropout=cfg["drop_rate"],
            qkv_bias=cfg["qkv_bias"])
        self.ff = FeedForward(cfg)
        self.norm1 = LayerNorm(cfg["emb_dim"])
        self.norm2 = LayerNorm(cfg["emb_dim"])
        self.drop_resid = nn.Dropout(cfg["drop_rate"])

    def forward(self, x):
        # Shortcut connection for attention block
        shortcut = x
        x = self.norm1(x)
        x = self.att(x)   # Shape [batch_size, num_tokens, emb_size]
        x = self.drop_resid(x)
        x = x + shortcut  # Add the original input back

        # Shortcut connection for feed-forward block
        shortcut = x
        x = self.norm2(x)
        x = self.ff(x)
        x = self.drop_resid(x)
        x = x + shortcut  # Add the original input back

        return x


class GPTModel(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.tok_emb = nn.Embedding(cfg["vocab_size"], cfg["emb_dim"])
        self.pos_emb = nn.Embedding(cfg["ctx_len"], cfg["emb_dim"])
        self.drop_emb = nn.Dropout(cfg["drop_rate"])

        self.trf_blocks = nn.Sequential(
            *[TransformerBlock(cfg) for _ in range(cfg["n_layers"])])

        self.final_norm = LayerNorm(cfg["emb_dim"])
        self.out_head = nn.Linear(cfg["emb_dim"], cfg["vocab_size"], bias=False)

    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_embeds = self.tok_emb(in_idx)
        pos_embeds = self.pos_emb(torch.arange(seq_len, device=in_idx.device))
        x = tok_embeds + pos_embeds  # Shape [batch_size, num_tokens, emb_size]
        x = self.drop_emb(x)
        x = self.trf_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits


def generate_text_simple(model, idx, max_new_tokens, context_size):
    # idx is (B, T) array of indices in the current context
    for _ in range(max_new_tokens):

        # Crop current context if it exceeds the supported context size
        # E.g., if LLM supports only 5 tokens, and the context size is 10
        # then only the last 5 tokens are used as context
        idx_cond = idx[:, -context_size:]

        # Get the predictions
        with torch.no_grad():
            logits = model(idx_cond)

        # Focus only on the last time step
        # (batch, n_token, vocab_size) becomes (batch, vocab_size)
        logits = logits[:, -1, :]

        # Get the idx of the vocab entry with the highest logits value
        idx_next = torch.argmax(logits, dim=-1, keepdim=True)  # (batch, 1)

        # Append sampled index to the running sequence
        idx = torch.cat((idx, idx_next), dim=1)  # (batch, n_tokens+1)

    return idx


if __name__ == "__main__":

    GPT_CONFIG_124M = {
        "vocab_size": 50257,  # Vocabulary size
        "ctx_len": 1024,      # Context length
        "emb_dim": 768,       # Embedding dimension
        "n_heads": 12,        # Number of attention heads
        "n_layers": 12,       # Number of layers
        "drop_rate": 0.1,     # Dropout rate
        "qkv_bias": False     # Query-Key-Value bias
    }

    torch.manual_seed(123)
    model = GPTModel(GPT_CONFIG_124M)
    model.eval()  # disable dropout

    start_context = "Hello, I am"

    tokenizer = tiktoken.get_encoding("gpt2")
    encoded = tokenizer.encode(start_context)
    encoded_tensor = torch.tensor(encoded).unsqueeze(0)

    print(f"\n{50*'='}\n{22*' '}IN\n{50*'='}")
    print("\nInput text:", start_context)
    print("Encoded input text:", encoded)
    print("encoded_tensor.shape:", encoded_tensor.shape)

    out = generate_text_simple(
        model=model,
        idx=encoded_tensor,
        max_new_tokens=10,
        context_size=GPT_CONFIG_124M["ctx_len"]
    )
    decoded_text = tokenizer.decode(out.squeeze(0).tolist())

    print(f"\n\n{50*'='}\n{22*' '}OUT\n{50*'='}")
    print("\nOutput:", out)
    print("Output length:", len(out[0]))
    print("Output text:", decoded_text)

import torch

GPT_CONFIG_124M = {
    "vocab_size": 50257,  # Vocabulary size
    "ctx_len": 256,       # Shortened context length (orig: 1024)
    "emb_dim": 768,       # Embedding dimension
    "n_heads": 12,        # Number of attention heads
    "n_layers": 12,       # Number of layers
    "drop_rate": 0.1,     # Dropout rate
    "qkv_bias": False     # Query-key-value bias
}

torch.manual_seed(123)
model = GPTModel(GPT_CONFIG_124M)
model.eval();  # Disable dropout during inference

We use dropout of 0.1 above, but it’s relatively common to train LLMs without dropout nowadays Modern LLMs also don’t use bias vectors in the nn.Linear layers for the query, key, and value matrices (unlike earlier GPT models), which is achieved by setting "qkv_bias": False We reduce the context length (ctx_len) of only 256 tokens to reduce the computational resource requirements for training the model, whereas the original 124 million parameter GPT-2 model used 1024 characters This is so that more readers will be able to follow and execute the code examples on their laptop computer However, please feel free to increase the ctx_len to 1024 tokens (this would not require any code changes) We will also load a model with a 1024 ctx_len later from pretrained weights

Next, we use the generate_text_simple function from the previous chapter to generate text In addition, we define two convenience functions, text_to_token_ids and token_ids_to_text, for converting between token and text representations that we use throughout this chapter

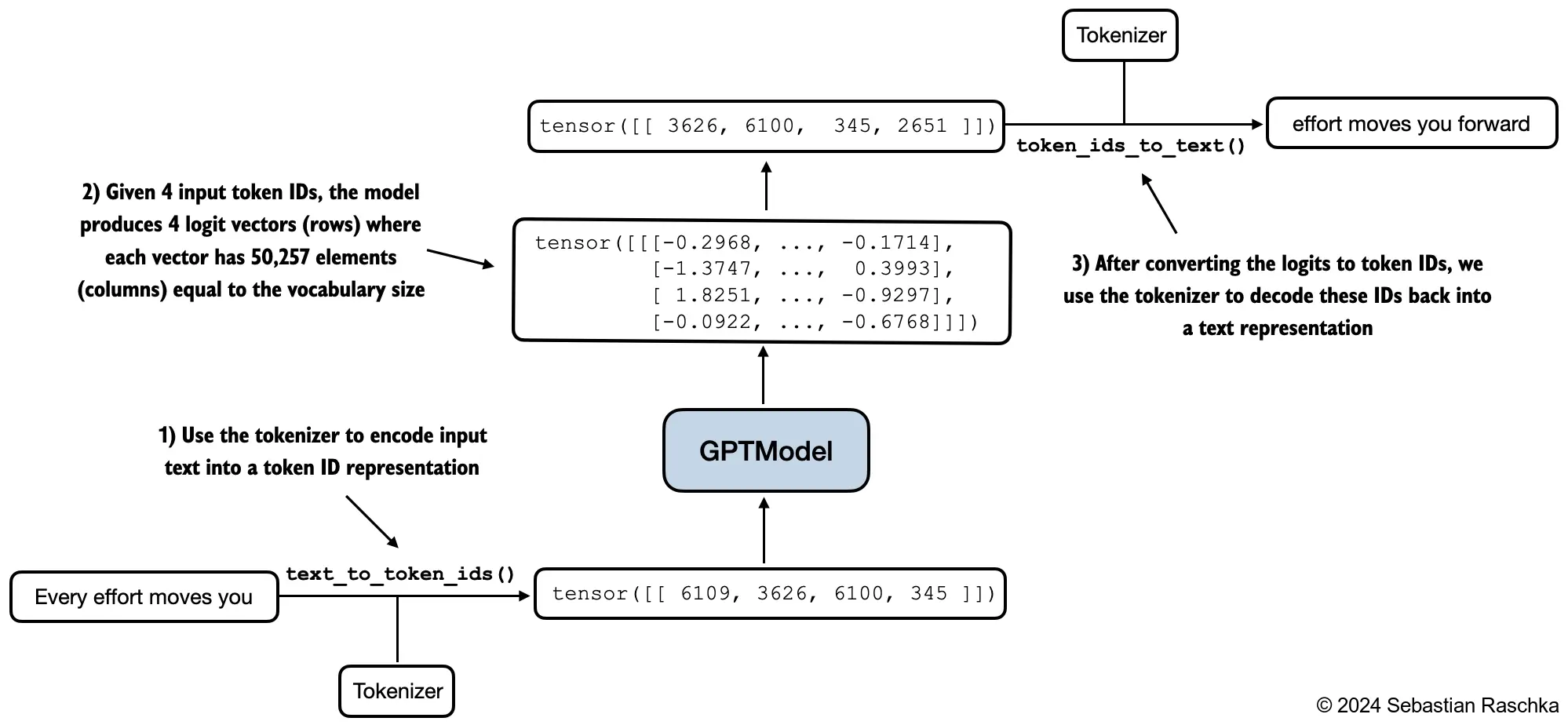
import tiktoken

def text_to_token_ids(text, tokenizer):
    encoded = tokenizer.encode(text, allowed_special={'<|endoftext|>'})
    encoded_tensor = torch.tensor(encoded).unsqueeze(0) # add batch dimension
    return encoded_tensor

def token_ids_to_text(token_ids, tokenizer):
    flat = token_ids.squeeze(0) # remove batch dimension
    return tokenizer.decode(flat.tolist())

start_context = "Every effort moves you"
tokenizer = tiktoken.get_encoding("gpt2")

token_ids = generate_text_simple(
    model=model,
    idx=text_to_token_ids(start_context, tokenizer),
    max_new_tokens=10,
    context_size=GPT_CONFIG_124M["ctx_len"]
)

print("Output text:\n", token_ids_to_text(token_ids, tokenizer))

Output text:
 Every effort moves you rentingetic wasnم refres RexMeCHicular stren

As we can see above, the model does not produce good text because it has not been trained yet How do we measure or capture what “good text” is, in a numeric form, to track it during training? The next subsection introduces metrics to calculate a loss metric for the generated outputs that we can use to measure the training progress The next chapters on finetuning LLMs will also introduce additional ways to measure model quality

41.10.1.2. Calculating the text generation loss: cross entropy, and perplexity

Suppose we have an inputs tensor containing the token IDs for 2 training examples (rows) Corresponding to the inputs, the targets contain the desired token IDs that we want the model to generate Notice that the targets are the inputs shifted by 1 position, as explained in chapter 2 when we implemented the data loader

inputs = torch.tensor([[16833, 3626, 6100],   # ["every effort moves",
                       [40,    1107, 588]])   #  "I really like"]

targets = torch.tensor([[3626, 6100, 345  ],  # [" effort moves you",
                        [588,  428,  11311]]) #  " really like chocolate"]

Feeding the inputs to the model, we obtain the logits vector for the 2 input examples that consist of 3 tokens each Each of the tokens is a 50,257-dimensional vector corresponding to the size of the vocabulary Applying the softmax function, we can turn the logits tensor into a tensor of the same dimension containing probability scores

with torch.no_grad():
    logits = model(inputs)

probas = torch.softmax(logits, dim=-1) # Probability of each token in vocabulary
print(probas.shape) # Shape: (batch_size, num_tokens, vocab_size)

torch.Size([2, 3, 50257])

The figure below, using a very small vocabulary for illustration purposes, outlines how we convert the probability scores back into text, which we discussed at the end of the previous chapter

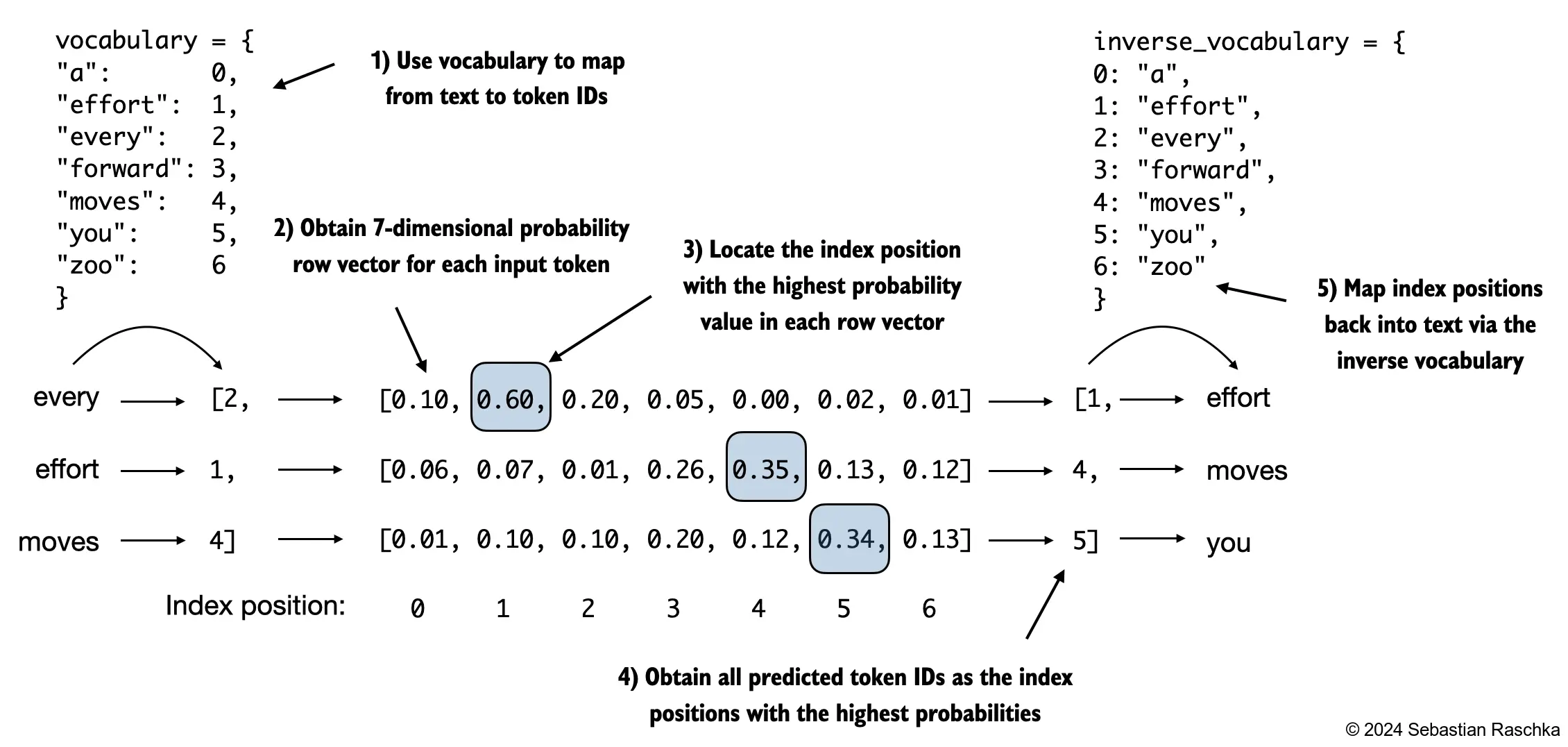
As discussed in the previous chapter, we can apply the argmax function to convert the probability scores into predicted token IDs The softmax function above produced a 50,257-dimensional vector for each token; the argmax function returns the position of the highest probability score in this vector, which is the predicted token ID for the given token

Since we have 2 input batches with 3 tokens each, we obtain 2 by 3 predicted token IDs:

token_ids = torch.argmax(probas, dim=-1, keepdim=True)
print("Token IDs:\n", token_ids)

Token IDs:
 tensor([[[16657],
         [  339],
         [42826]],

        [[49906],
         [29669],
         [41751]]])

If we decode these tokens, we find that these are quite different from the tokens we want the model to predict, namely the target tokens:

print(f"Targets batch 1: {token_ids_to_text(targets[0], tokenizer)}")
print(f"Outputs batch 1: {token_ids_to_text(token_ids[0].flatten(), tokenizer)}")

Targets batch 1:  effort moves you
Outputs batch 1:  Armed heNetflix

That’s because the model wasn’t trained yet To train the model, we need to know how far it is away from the correct predictions (targets)

The token probabilities corresponding to the target indices are as follows:

batch_idx = 0
target_probas_1 = probas[batch_idx, [0, 1, 2], targets[batch_idx]]
print("Batch 1:", target_probas_1)

batch_idx = 1
target_probas_2 = probas[1, [0, 1, 2], targets[1]]
print("Batch 2:", target_probas_2)

Batch 1: tensor([7.4541e-05, 3.1061e-05, 1.1563e-05])
Batch 2: tensor([3.9836e-05, 1.6783e-05, 4.7559e-06])

We want to maximize all these values, bringing them close to a probability of 1 In mathematical optimization, it is easier to maximize the logarithm of the probability score than the probability score itself

# Compute logarithm of all token probabilities
log_probas = torch.log(torch.cat((target_probas_1, target_probas_2)))
print(log_probas)

tensor([ -9.5042, -10.3796, -11.3677, -10.1308, -10.9951, -12.2561])

Next, we compute the average log probability:

# Calculate the average probability for each token
avg_log_probas = torch.mean(log_probas)
print(avg_log_probas)

tensor(-10.7722)

The goal is to make this average log probability as large as possible by optimizing the model weights Due to the log, the largest possible value is 0, and we are currently far away from 0

In deep learning, instead of maximizing the average log-probability, it’s a standard convention to minimize the negative average log-probability value; in our case, instead of maximizing -10.7722 so that it approaches 0, in deep learning, we would minimize 10.7722 so that it approaches 0 The value negative of -10.7722, i.e., 10.7722, is also called cross entropy loss in deep learning

neg_avg_log_probas = avg_log_probas * -1
print(neg_avg_log_probas)

tensor(10.7722)

PyTorch already implements a cross_entropy function that carries out the previous steps

Before we apply the cross entropy function, let’s check the shape of the logits and targets

# Logits have shape (batch_size, num_tokens, vocab_size)
print("Logits shape:", logits.shape)

# Targets have shape (batch_size, num_tokens)
print("Targets shape:", targets.shape)

Logits shape: torch.Size([2, 3, 50257])
Targets shape: torch.Size([2, 3])

For the cross entropy_loss function in PyTorch, we want to flatten these tensors by combining them over the batch dimension:

logits_flat = logits.flatten(0, 1)
targets_flat = targets.flatten()

print("Flattened logits:", logits_flat.shape)
print("Flattened targets:", targets_flat.shape)

Flattened logits: torch.Size([6, 50257])
Flattened targets: torch.Size([6])

Note that the targets are the token IDs, which also represent the index positions in the logits tensors that we want to maximize The cross_entropy function in PyTorch will automatically take care of applying the softmax and log-probability computation internally over those token indices in the logits that are to be maximized

loss = torch.nn.functional.cross_entropy(logits_flat, targets_flat)
print(loss)

tensor(10.7722)

A concept related to the cross entropy loss is the perplexity of an LLM The perplexity is simply the exponential of the cross entropy loss

perplexity = torch.exp(loss)
print(perplexity)

tensor(47678.8633)

The perplexity is often considered more interpretable because it can be understood as the effective vocabulary size that the model is uncertain about at each step (in the example above, that’d be 47,678 words or tokens) In other words, perplexity provides a measure of how well the probability distribution predicted by the model matches the actual distribution of the words in the dataset Similar to the loss, a lower perplexity indicates that the model predictions are closer to the actual distribution

41.10.1.3. Calculating the training and validation set losses

We use a relatively small dataset for training the LLM (in fact, only one short story) The reasons are: You can run the code examples in a few minutes on a laptop computer without a suitable GPU The training finishes relatively fast (minutes instead of weeks), which is good for educational purposes We use a text from the public domain, which can be included in this GitHub repository without violating any usage rights or bloating the repository size

For example, Llama 2 7B required 184,320 GPU hours on A100 GPUs to be trained on 2 trillion tokens At the time of this writing, the hourly cost of an 8xA100 cloud server at AWS is approximately \\(30 So, via an off-the-envelope calculation, training this LLM would cost 184,320 / 8 * \\\)30 = \$690,000

Below, we use the same dataset we used in chapter 2

import os
import urllib.request

file_path = "the-verdict.txt"
url = "https://static-1300131294.cos.ap-shanghai.myqcloud.com/images/llm/the-verdict.txt"

if not os.path.exists(file_path):
    with urllib.request.urlopen(url) as response:
        text_data = response.read().decode('utf-8')
    with open(file_path, "w", encoding="utf-8") as file:
        file.write(text_data)
else:
    with open(file_path, "r", encoding="utf-8") as file:
        text_data = file.read()

A quick check that the text loaded ok by printing the first and last 100 words

# First 100 characters
print(text_data[:99])

I HAD always thought Jack Gisburn rather a cheap genius--though a good fellow enough--so it was no 

# Last 100 characters
print(text_data[-99:])

it for me! The Strouds stand alone, and happen once--but there's no exterminating our kind of art."

total_char = len(text_data)
total_tokens = len(tokenizer.encode(text_data))

print("Characters:", total_char)
print("Tokens:", total_tokens)

Characters: 20479
Tokens: 5145

With 5,145 tokens, the text is very short for training an LLM, but again, it’s for educational purposes (we will also load pretrained weights later)

Next, we divide the dataset into a training and a validation set and use the data loaders from chapter 2 to prepare the batches for LLM training For visualization purposes, the figure below assumes a max_length=6, but for the training loader, we set the max_length equal to the context length that the LLM supports The figure below only shows the input tokens for simplicity Since we train the LLM to predict the next word in the text, the targets look the same as these inputs, except that the targets are shifted by one position

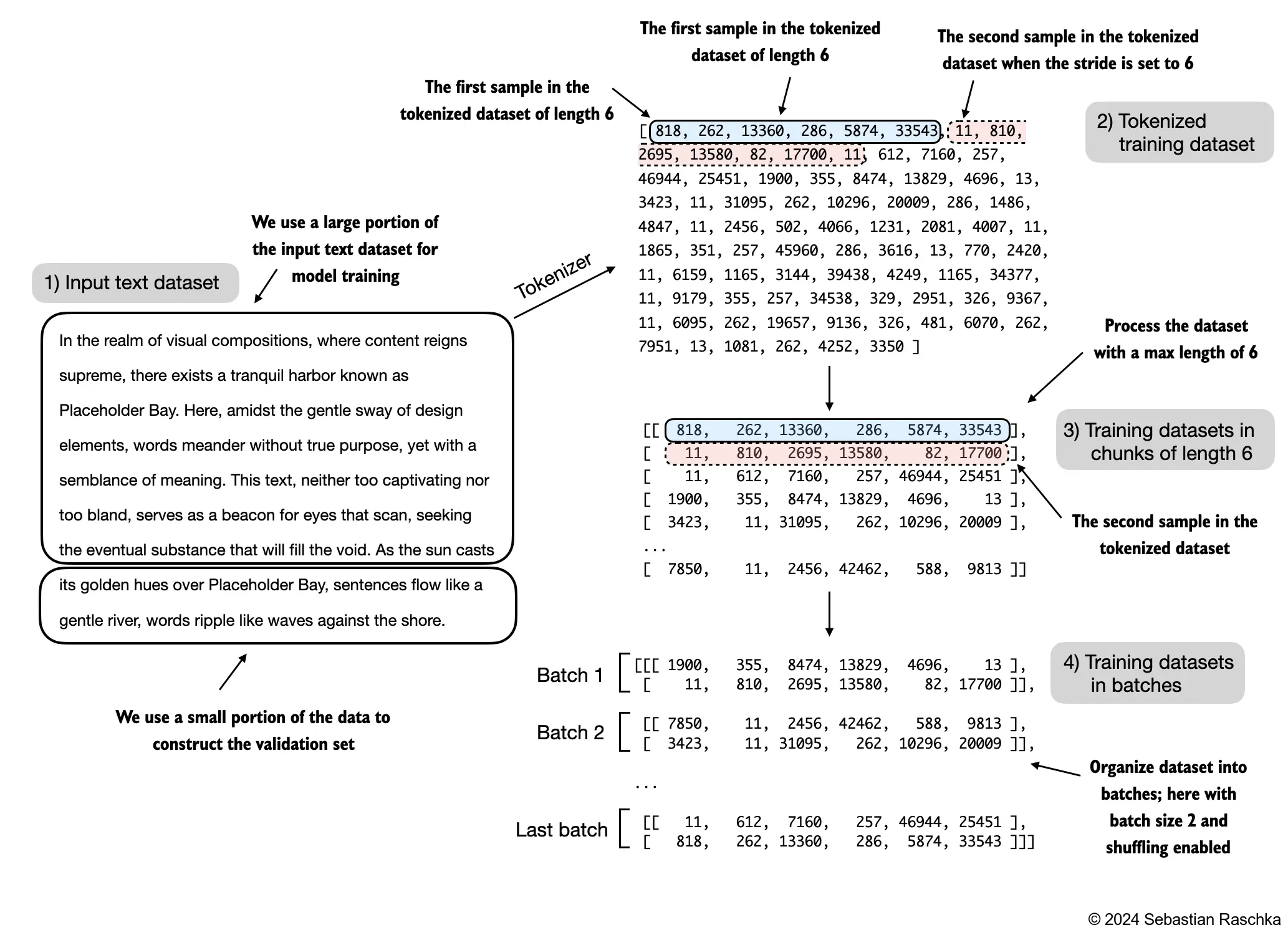
# Train/validation ratio
train_ratio = 0.90
split_idx = int(train_ratio * len(text_data))
train_data = text_data[:split_idx]
val_data = text_data[split_idx:]


torch.manual_seed(123)

train_loader = create_dataloader_v1(
    train_data,
    batch_size=2,
    max_length=GPT_CONFIG_124M["ctx_len"],
    stride=GPT_CONFIG_124M["ctx_len"],
    drop_last=True,
    shuffle=True
)

val_loader = create_dataloader_v1(
    val_data,
    batch_size=2,
    max_length=GPT_CONFIG_124M["ctx_len"],
    stride=GPT_CONFIG_124M["ctx_len"],
    drop_last=False,
    shuffle=False
)

# Sanity check

if total_tokens * (train_ratio) < GPT_CONFIG_124M["ctx_len"]:
    print("Not enough tokens for the training loader. "
          "Try to lower the `GPT_CONFIG_124M['ctx_len']` or "
          "increase the `training_ratio`")

if total_tokens * (1-train_ratio) < GPT_CONFIG_124M["ctx_len"]:
    print("Not enough tokens for the validation loader. "
          "Try to lower the `GPT_CONFIG_124M['ctx_len']` or "
          "decrease the `training_ratio`")

We use a relatively small batch size to reduce the computational resource demand, and because the dataset is very small to begin with Llama 2 7B was trained with a batch size of 1024, for example

An optional check that the data was loaded correctly:

print("Train loader:")
for x, y in train_loader:
    print(x.shape, y.shape)

print("\nValidation loader:")
for x, y in val_loader:
    print(x.shape, y.shape)

Train loader:
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])
torch.Size([2, 256]) torch.Size([2, 256])

Validation loader:
torch.Size([2, 256]) torch.Size([2, 256])

Another optional check that the token sizes are in the expected ballpark:

train_tokens = 0
for input_batch, target_batch in train_loader:
    train_tokens += input_batch.numel()

val_tokens = 0
for input_batch, target_batch in val_loader:
    val_tokens += input_batch.numel()

print("Training tokens:", train_tokens)
print("Validation tokens:", val_tokens)
print("All tokens:", train_tokens + val_tokens)

Training tokens: 4608
Validation tokens: 512
All tokens: 5120

Next, we implement a utility function to calculate the cross entropy loss of a given batch In addition, we implement a second utility function to compute the loss for a user-specified number of batches in a data loader

def calc_loss_batch(input_batch, target_batch, model, device):
    input_batch, target_batch = input_batch.to(device), target_batch.to(device)

    logits = model(input_batch)
    logits = logits.flatten(0, 1)
    loss = torch.nn.functional.cross_entropy(logits, target_batch.flatten())
    return loss


def calc_loss_loader(data_loader, model, device, num_batches=None):
    total_loss = 0.
    if num_batches is None:
        num_batches = len(data_loader)
    else:
        # Reduce the number of batches to match the total number of batches in the data loader
        # if num_batches exceeds the number of batches in the data loader
        num_batches = min(num_batches, len(data_loader))
    for i, (input_batch, target_batch) in enumerate(data_loader):
        if i < num_batches:
            loss = calc_loss_batch(input_batch, target_batch, model, device)
            total_loss += loss.item()
        else:
            break
    return total_loss / num_batches

If you have a machine with a CUDA-supported GPU, the LLM will train on the GPU without making any changes to the code Via the device setting, we ensure that the data is loaded onto the same device as the LLM model

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device) # no assignment model = model.to(device) necessary for nn.Module classes


torch.manual_seed(123) # For reproducibility due to the shuffling in the data loader
train_loss = calc_loss_loader(train_loader, model, device)
val_loss = calc_loss_loader(val_loader, model, device)

print("Training loss:", train_loss)
print("Validation loss:", val_loss)

Training loss: 10.98758347829183
Validation loss: 10.98110580444336

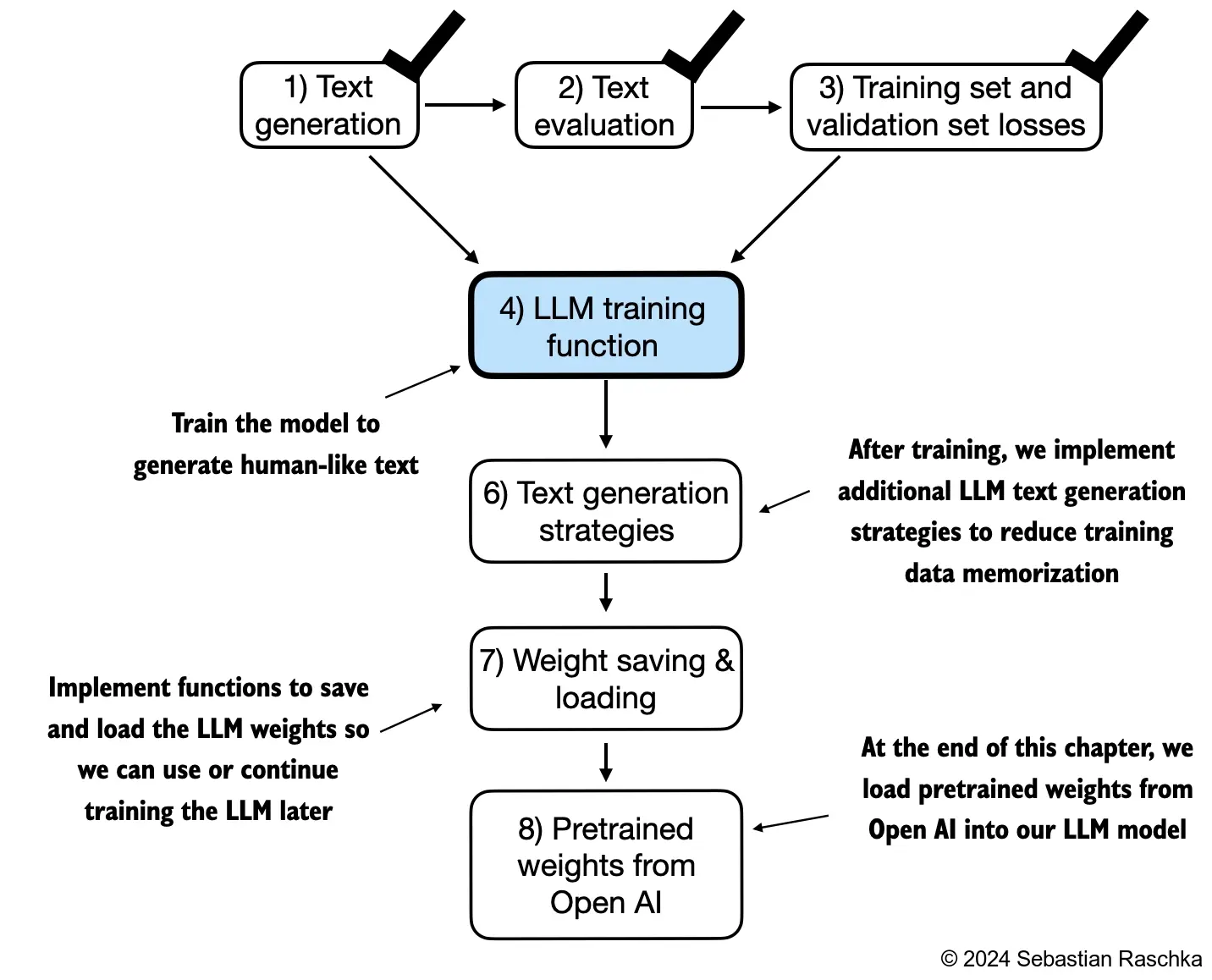
41.10.2. Training an LLM

In this section, we finally implement the code for training the LLM ( We focus on a simple training function )

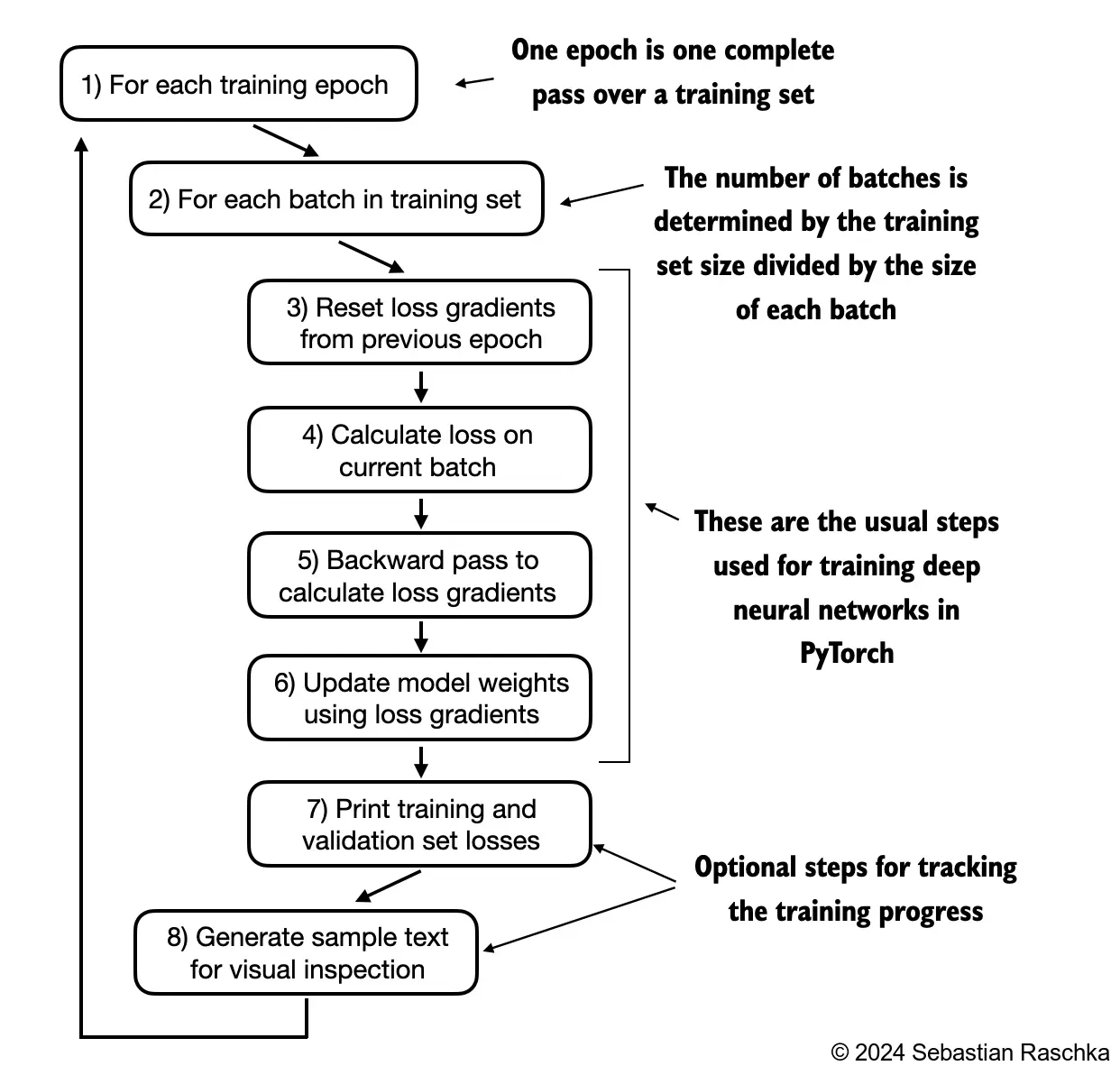
def train_model_simple(model, train_loader, val_loader, optimizer, device, num_epochs,
                       eval_freq, eval_iter, start_context):
    # Initialize lists to track losses and tokens seen
    train_losses, val_losses, track_tokens_seen = [], [], []
    tokens_seen, global_step = 0, -1

    # Main training loop
    for epoch in range(num_epochs):
        model.train()  # Set model to training mode
        
        for input_batch, target_batch in train_loader:
            optimizer.zero_grad() # Reset loss gradients from previous epoch
            loss = calc_loss_batch(input_batch, target_batch, model, device)
            loss.backward() # Calculate loss gradients
            optimizer.step() # Update model weights using loss gradients
            tokens_seen += input_batch.numel()
            global_step += 1

            # Optional evaluation step
            if global_step % eval_freq == 0:
                train_loss, val_loss = evaluate_model(
                    model, train_loader, val_loader, device, eval_iter)
                train_losses.append(train_loss)
                val_losses.append(val_loss)
                track_tokens_seen.append(tokens_seen)
                print(f"Ep {epoch+1} (Step {global_step:06d}): "
                      f"Train loss {train_loss:.3f}, Val loss {val_loss:.3f}")

        # Print a sample text after each epoch
        generate_and_print_sample(
            model, train_loader.dataset.tokenizer, device, start_context
        )

    return train_losses, val_losses, track_tokens_seen


def evaluate_model(model, train_loader, val_loader, device, eval_iter):
    model.eval()
    with torch.no_grad():
        train_loss = calc_loss_loader(train_loader, model, device, num_batches=eval_iter)
        val_loss = calc_loss_loader(val_loader, model, device, num_batches=eval_iter)
    model.train()
    return train_loss, val_loss


def generate_and_print_sample(model, tokenizer, device, start_context):
    model.eval()
    context_size = model.pos_emb.weight.shape[0]
    encoded = text_to_token_ids(start_context, tokenizer).to(device)
    with torch.no_grad():
        token_ids = generate_text_simple(
            model=model, idx=encoded,
            max_new_tokens=50, context_size=context_size
        )
        decoded_text = token_ids_to_text(token_ids, tokenizer)
        print(decoded_text.replace("\n", " "))  # Compact print format
    model.train()

Now, let’s train the LLM using the training function defined above:

torch.manual_seed(123)
model = GPTModel(GPT_CONFIG_124M)
model.to(device)
optimizer = torch.optim.AdamW(model.parameters(), lr=5e-4, weight_decay=0.1)

num_epochs = 10
train_losses, val_losses, tokens_seen = train_model_simple(
    model, train_loader, val_loader, optimizer, device,
    num_epochs=num_epochs, eval_freq=5, eval_iter=5,
    start_context="Every effort moves you",
)

Ep 1 (Step 000000): Train loss 9.558, Val loss 9.856
Ep 1 (Step 000005): Train loss 7.651, Val loss 8.051
Every effort moves you,,,,,,,,,,,,.                                     
Ep 2 (Step 000010): Train loss 6.421, Val loss 6.812
Ep 2 (Step 000015): Train loss 5.913, Val loss 6.559
Every effort moves you, and, and,, and,,,,, and, and,,,, and,,,, and, and,, and,,,, and,, and,,,,, and,,,,,,
Ep 3 (Step 000020): Train loss 5.680, Val loss 6.490
Ep 3 (Step 000025): Train loss 5.557, Val loss 6.602
Every effort moves you, and, and the picture.                             ", and, and the, and the, and, and,
Ep 4 (Step 000030): Train loss 5.204, Val loss 6.508
Ep 4 (Step 000035): Train loss 4.865, Val loss 6.420
Every effort moves you, and I had a a a--I to the picture. "I. I had the picture. "I had the picture. I had the the picture. I had the the picture. "I had the picture. "
Ep 5 (Step 000040): Train loss 4.332, Val loss 6.328
Every effort moves you, I was a and I was a little to the picture.                                     
Ep 6 (Step 000045): Train loss 4.295, Val loss 6.221
Ep 6 (Step 000050): Train loss 3.268, Val loss 6.184
Every effort moves you know to see the end of the Riv I felt--the a little of the last: "                               
Ep 7 (Step 000055): Train loss 2.880, Val loss 6.129
Ep 7 (Step 000060): Train loss 2.820, Val loss 6.194
Every effort moves you know the fact of a little a--I was his painting.                                     
Ep 8 (Step 000065): Train loss 2.260, Val loss 6.236
Ep 8 (Step 000070): Train loss 1.754, Val loss 6.260
Every effort moves you know," was one of the picture for nothing--I turned Mrs.                                    
Ep 9 (Step 000075): Train loss 1.447, Val loss 6.319
Ep 9 (Step 000080): Train loss 1.120, Val loss 6.310
Every effort moves you?"               "I looked--and me."         He placed them at my elbow and I looked up his pictures--because he's I had
Ep 10 (Step 000085): Train loss 0.762, Val loss 6.372
Every effort moves you?"  "Yes--quite insensible to the irony. She wanted him vindicated--and by me!"  He laughed again, and threw back his head to look up at the sketch of the donkey. "There were days when I

import matplotlib.pyplot as plt

def plot_losses(epochs_seen, tokens_seen, train_losses, val_losses):
    fig, ax1 = plt.subplots(figsize=(5, 3))

    # Plot training and validation loss against epochs
    ax1.plot(epochs_seen, train_losses, label="Training loss")
    ax1.plot(epochs_seen, val_losses, linestyle="-.", label="Validation loss")
    ax1.set_xlabel("Epochs")
    ax1.set_ylabel("Loss")
    ax1.legend(loc="upper right")

    # Create a second x-axis for tokens seen
    ax2 = ax1.twiny()  # Create a second x-axis that shares the same y-axis
    ax2.plot(tokens_seen, train_losses, alpha=0)  # Invisible plot for aligning ticks
    ax2.set_xlabel("Tokens seen")

    fig.tight_layout()  # Adjust layout to make room
    plt.savefig("loss-plot.pdf")
    plt.show()

epochs_tensor = torch.linspace(0, num_epochs, len(train_losses))
plot_losses(epochs_tensor, tokens_seen, train_losses, val_losses)

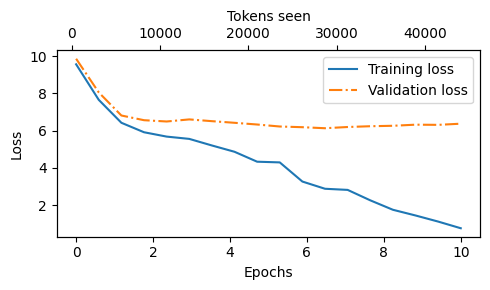
Looking at the results above, we can see that the model starts out generating incomprehensible strings of words, whereas towards the end, it’s able to produce grammatically more or less correct sentences However, based on the training and validation set losses, we can see that the model starts overfitting If we were to check a few passages it writes towards the end, we would find that they are contained in the training set verbatim -it simply memorizes the training data Later, we will cover decoding strategies that can mitigate this memorization by a certain degree Note that the overfitting here occurs because we have a very, very small training set, and we iterate over it so many times The LLM training here primarily serves educational purposes; we mainly want to see that the model can learn to produce coherent text Instead of spending weeks or months on training this model on vast amounts of expensive hardware, we load pretrained weights later

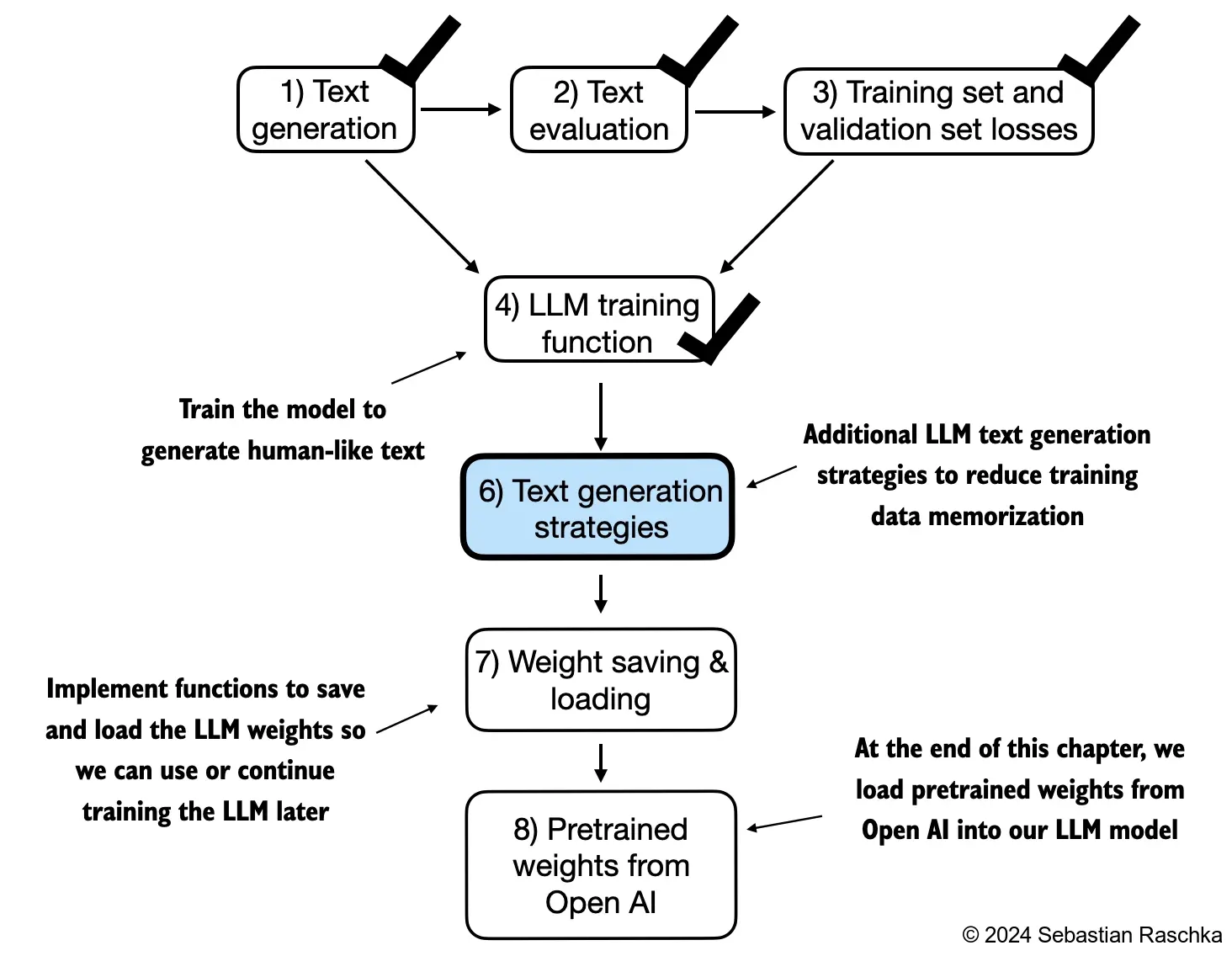
41.10.3. Decoding strategies to control randomness

Inference is relatively cheap with a relatively small LLM as the GPT model we trained above, so there’s no need to use a GPU for it in case you used a GPU for training it above Using the generate_text_simple function (from the previous chapter) that we used earlier inside the simple training function, we can generate new text one word (or token) at a time As explained in sections above, the next generated token is the token corresponding to the largest probability score among all tokens in the vocabulary

model.to("cpu")
model.eval()

tokenizer = tiktoken.get_encoding("gpt2")

token_ids = generate_text_simple(
    model=model,
    idx=text_to_token_ids("Every effort moves you", tokenizer),
    max_new_tokens=25,
    context_size=GPT_CONFIG_124M["ctx_len"]
)

print("Output text:\n", token_ids_to_text(token_ids, tokenizer))

Output text:
 Every effort moves you?"

"Yes--quite insensible to the irony. She wanted him vindicated--and by me!"

Even if we execute the generate_text_simple function above multiple times, the LLM will always generate the same outputs We now introduce two concepts, so-called decoding strategies, to modify the generate_text_simple: temperature scaling and top-k sampling These will allow the model to control the randomness and diversity of the generated text

41.10.3.1. Temperature scaling

Previously, we always sampled the token with the highest probability as the next token using torch.argmax To add variety, we can sample the next token using The torch.multinomial(probs, num_samples=1), sampling from a probability distribution Here, each index’s chance of being picked corresponds to its probability in the input tensor

Here’s a little recap of generating the next token, assuming a very small vocabulary for illustration purposes:

vocab = { 
    "closer": 0,
    "every": 1, 
    "effort": 2, 
    "forward": 3,
    "inches": 4,
    "moves": 5, 
    "pizza": 6,
    "toward": 7,
    "you": 8,
} 

inverse_vocab = {v: k for k, v in vocab.items()}

# Suppose input is "every effort moves you", and the LLM
# returns the following logits for the next token:
next_token_logits = torch.tensor(
    [4.51, 0.89, -1.90, 6.75, 1.63, -1.62, -1.89, 6.28, 1.79]
)

probas = torch.softmax(next_token_logits, dim=0)
next_token_id = torch.argmax(probas).item()

# The next generated token is then as follows:
print(inverse_vocab[next_token_id])

forward

torch.manual_seed(123)
next_token_id = torch.multinomial(probas, num_samples=1).item()
print(inverse_vocab[next_token_id])

forward

def print_sampled_tokens(probas):
    torch.manual_seed(123) # Manual seed for reproducibility
    sample = [torch.multinomial(probas, num_samples=1).item() for i in range(1_000)]
    sampled_ids = torch.bincount(torch.tensor(sample))
    for i, freq in enumerate(sampled_ids):
        print(f"{freq} x {inverse_vocab[i]}")

print_sampled_tokens(probas)

73 x closer
0 x every
0 x effort
582 x forward
2 x inches
0 x moves
0 x pizza
343 x toward

Instead of determining the most likely token via torch.argmax, we use torch.multinomial(probas, num_samples=1) to determine the most likely token by sampling from the softmax distribution For illustration purposes, let’s see what happens when we sample the next token 1,000 times using the original softmax probabilities:

We can control the distribution and selection process via a concept called temperature scaling “Temperature scaling” is just a fancy word for dividing the logits by a number greater than 0 Temperatures greater than 1 will result in more uniformly distributed token probabilities after applying the softmax Temperatures smaller than 1 will result in more confident (sharper or more peaky) distributions after applying the softmax

def softmax_with_temperature(logits, temperature):
    scaled_logits = logits / temperature
    return torch.softmax(scaled_logits, dim=0)

# Temperature values
temperatures = [1, 0.1, 5]  # Original, higher confidence, and lower confidence

# Calculate scaled probabilities
scaled_probas = [softmax_with_temperature(next_token_logits, T) for T in temperatures]

# Plotting
x = torch.arange(len(vocab))
bar_width = 0.15

fig, ax = plt.subplots(figsize=(5, 3))
for i, T in enumerate(temperatures):
    rects = ax.bar(x + i * bar_width, scaled_probas[i], bar_width, label=f'Temperature = {T}')

ax.set_ylabel('Probability')
ax.set_xticks(x)
ax.set_xticklabels(vocab.keys(), rotation=90)
ax.legend()

plt.tight_layout()
plt.savefig("temperature-plot.pdf")
plt.show()

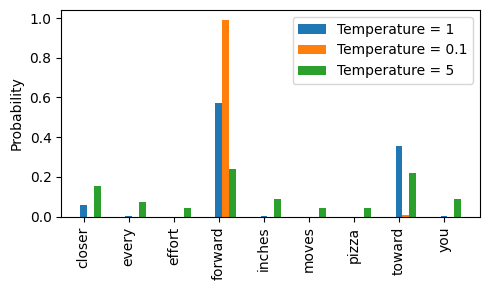
We can see that the rescaling via temperature 0.1 results in a sharper distribution, approaching torch.argmax, such that the most likely word is almost always selected:

print_sampled_tokens(scaled_probas[1])

0 x closer
0 x every
0 x effort
985 x forward
0 x inches
0 x moves
0 x pizza
15 x toward

The rescaled probabilities via temperature 5 are more uniformly distributed:

print_sampled_tokens(scaled_probas[2])

165 x closer
75 x every
42 x effort
239 x forward
71 x inches
46 x moves
32 x pizza
227 x toward
103 x you

Assuming an LLM input “every effort moves you”, using the approach above can sometimes result in nonsensical texts, such as “every effort moves you pizza”, 3.2% of the time (32 out of 1000 times)

41.10.3.2. Top-k sampling

To be able to use higher temperatures to increase output diversity and to reduce the probability of nonsensical sentences, we can restrict the sampled tokens to the top-k most likely tokens:

In code, we can implement this as follows:

top_k = 3
top_logits, top_pos = torch.topk(next_token_logits, top_k)

print("Top logits:", top_logits)
print("Top positions:", top_pos)

Top logits: tensor([6.7500, 6.2800, 4.5100])
Top positions: tensor([3, 7, 0])

new_logits = torch.where(
    condition=next_token_logits < top_logits[-1],
    input=torch.tensor(float('-inf')), 
    other=next_token_logits
)

print(new_logits)

tensor([4.5100,   -inf,   -inf, 6.7500,   -inf,   -inf,   -inf, 6.2800,   -inf])

topk_probas = torch.softmax(new_logits, dim=0)
print(topk_probas)

tensor([0.0615, 0.0000, 0.0000, 0.5775, 0.0000, 0.0000, 0.0000, 0.3610, 0.0000])

41.10.3.3. Modifying the text generation function

The previous two subsections introduced temperature sampling and top-k sampling Let’s use these two concepts to modify the generate_simple function we used to generate text via the LLM earlier, creating a new generate function:

def generate(model, idx, max_new_tokens, context_size, temperature, top_k=None):

    # For-loop is the same as before: Get logits, and only focus on last time step
    for _ in range(max_new_tokens):
        idx_cond = idx[:, -context_size:]
        with torch.no_grad():
            logits = model(idx_cond)
        logits = logits[:, -1, :]

        # New: Filter logits with top_k sampling
        if top_k is not None:
            # Keep only top_k values
            top_logits, _ = torch.topk(logits, top_k)
            min_val = top_logits[:, -1]
            logits = torch.where(logits < min_val, torch.tensor(float('-inf')).to(logits.device), logits)

        # New: Apply temperature scaling
        if temperature > 0.0:
            logits = logits / temperature

            # Apply softmax to get probabilities
            probs = torch.softmax(logits, dim=-1)  # (batch_size, context_len)

            # Sample from the distribution
            idx_next = torch.multinomial(probs, num_samples=1)  # (batch_size, 1)

        # Otherwise same as before: get idx of the vocab entry with the highest logits value
        else:
            idx_next = torch.argmax(logits, dim=-1, keepdim=True)  # (batch_size, 1)

        # Same as before: append sampled index to the running sequence
        idx = torch.cat((idx, idx_next), dim=1)  # (batch_size, num_tokens+1)

    return idx

torch.manual_seed(123)

token_ids = generate(
    model=model,
    idx=text_to_token_ids("Every effort moves you", tokenizer),
    max_new_tokens=20,
    context_size=GPT_CONFIG_124M["ctx_len"],
    top_k=10,
    temperature=1.5
)

print("Output text:\n", token_ids_to_text(token_ids, tokenizer))

Output text:
 Every effort moves you?"," was down surprise. It is to face watching me by his painting him back to my work

41.10.4. Loading and saving model weights in PyTorch

Training LLMs is computationally expensive, so it’s crucial to be able to save and load LLM weights

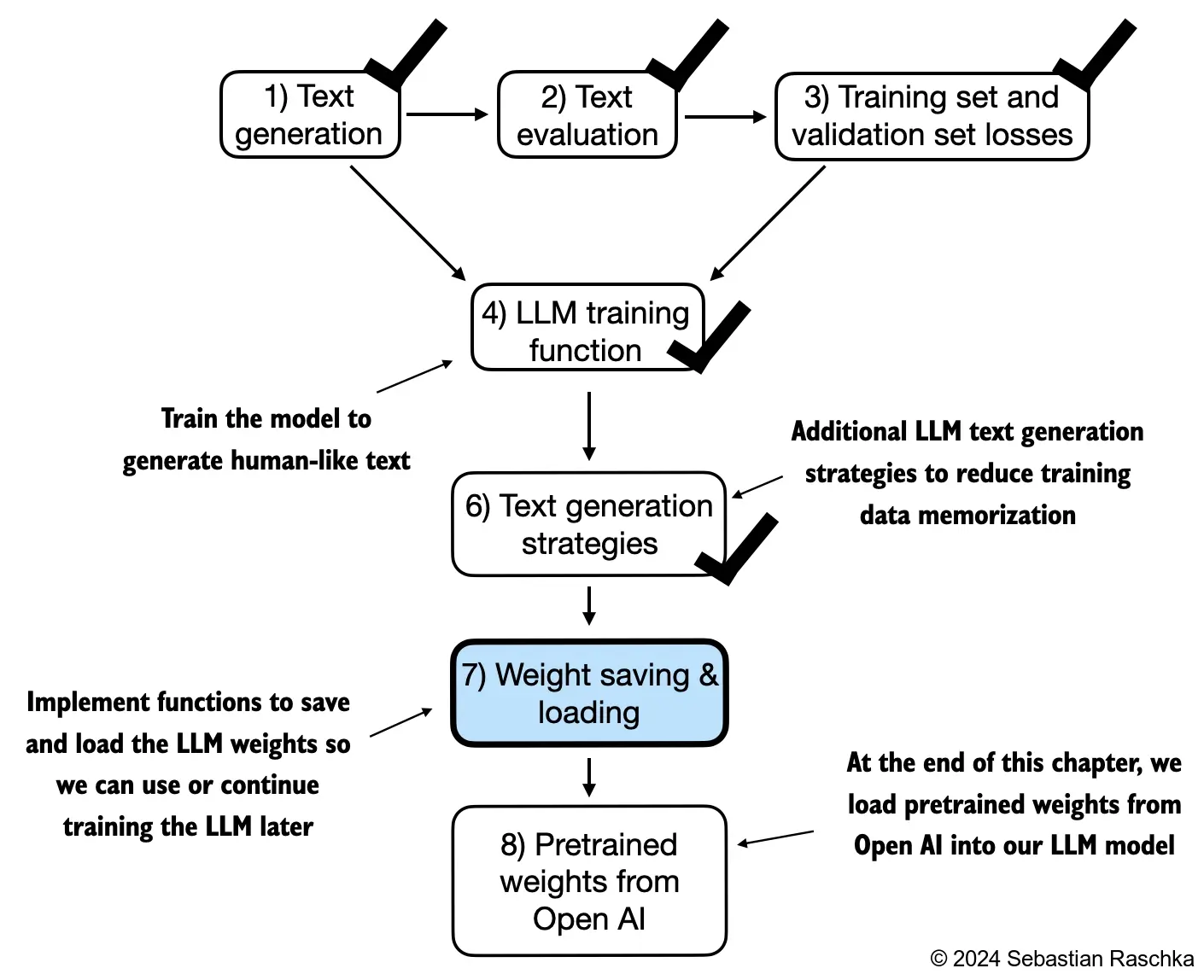
The recommended way in PyTorch is to save the model weights, the so-called state_dict via by applying the torch.save function to the .state_dict() method:

torch.save(model.state_dict(), "model.pth")

Then we can load the model weights into a new GPTModel model instance as follows:

model = GPTModel(GPT_CONFIG_124M)
model.load_state_dict(torch.load("model.pth"))
model.eval();

It’s common to train LLMs with adaptive optimizers like Adam or AdamW instead of regular SGD These adaptive optimizers store additional parameters for each model weight, so it makes sense to save them as well in case we plan to continue the pretraining later:

torch.save({
    "model_state_dict": model.state_dict(),
    "optimizer_state_dict": optimizer.state_dict(),
    }, 
    "model_and_optimizer.pth"
)

checkpoint = torch.load("model_and_optimizer.pth")

model = GPTModel(GPT_CONFIG_124M)
model.load_state_dict(checkpoint["model_state_dict"])

optimizer = torch.optim.AdamW(model.parameters(), lr=5e-4, weight_decay=0.1)
optimizer.load_state_dict(checkpoint["optimizer_state_dict"])
model.train();

41.10.5. Loading pretrained weights from Open AI

Fortunately, we don’t have to spend tens to hundreds of thousands of dollars to pretrain the model on a large pretraining corpus but can load the pretrained weights provided by OpenAI

First, some boilerplate code to download the files from OpenAI and load the weights into Python Since OpenAI used TensorFlow, we will have to install and use TensorFlow for loading the weights; tqdm is a progress bar library Uncomment and run the next cell to install the required libraries

# pip install tensorflow tqdm

print("TensorFlow version:", version("tensorflow"))
print("tqdm version:", version("tqdm"))

TensorFlow version: 2.15.0
tqdm version: 4.66.1

# Relative import from the gpt_download.py contained in this folder
from gpt_download import download_and_load_gpt2

We can then download the model weights for the 124 million parameter model as follows:

hparams, params = download_and_load_gpt2(model_size="124M", models_dir="gpt2")

File already exists and is up-to-date: gpt2/124M/checkpoint
File already exists and is up-to-date: gpt2/124M/encoder.json
File already exists and is up-to-date: gpt2/124M/hparams.json
File already exists and is up-to-date: gpt2/124M/model.ckpt.data-00000-of-00001
File already exists and is up-to-date: gpt2/124M/model.ckpt.index
File already exists and is up-to-date: gpt2/124M/model.ckpt.meta
File already exists and is up-to-date: gpt2/124M/vocab.bpe

print("Settings:", hparams)

Settings: {'n_vocab': 50257, 'n_ctx': 1024, 'n_embd': 768, 'n_head': 12, 'n_layer': 12}

print("Parameter dictionary keys:", params.keys())

Parameter dictionary keys: dict_keys(['blocks', 'b', 'g', 'wpe', 'wte'])

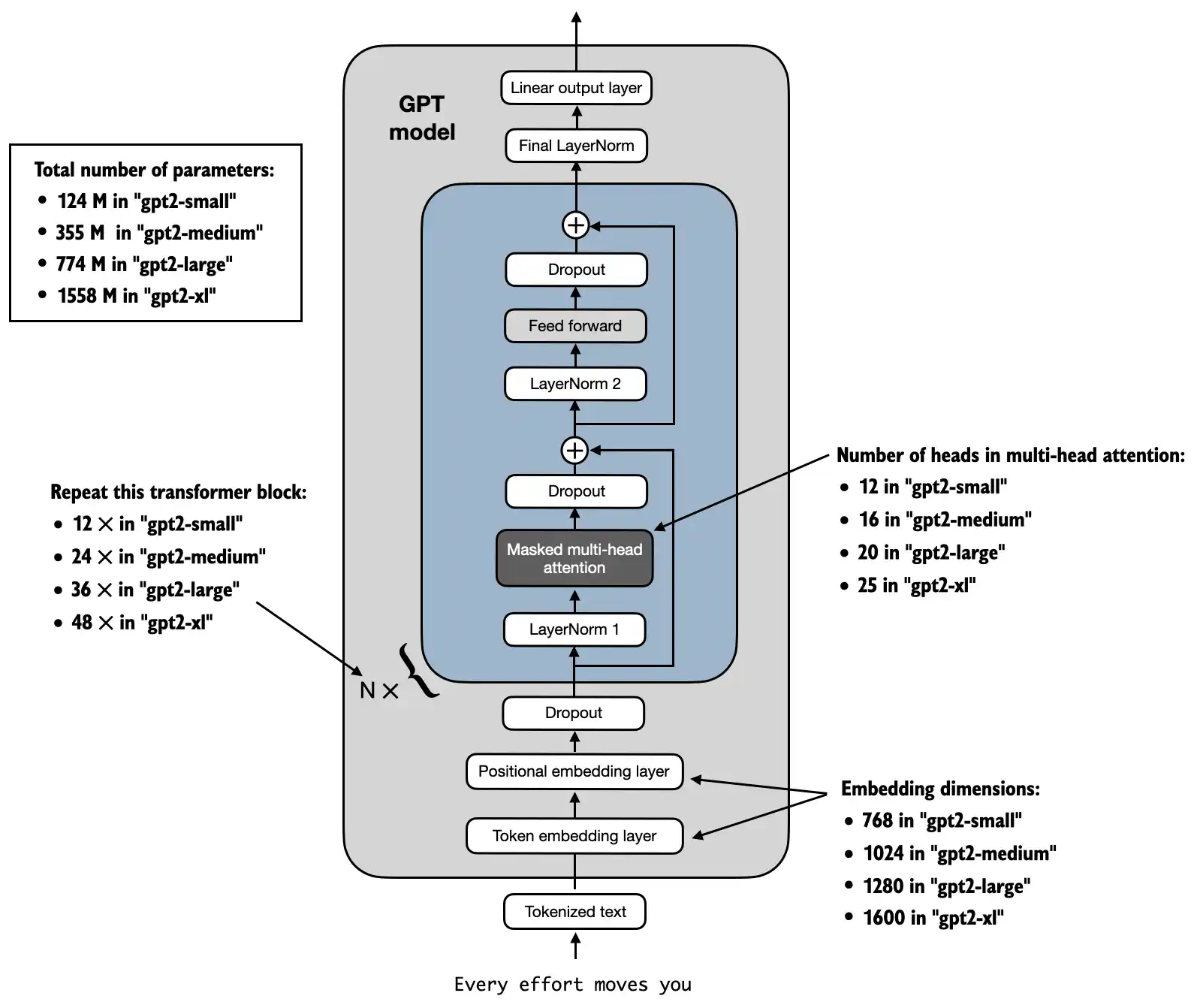
Alternatively, “355M”, “774M”, and “1558M” are also supported model_size arguments The difference between these differently sized models is summarized in the figure below:

Above, we loaded the 124M GPT-2 model weights into Python, however we still need to transfer them into our GPTModel instance First, we initialize a new GPTModel instance Note that the original GPT model initialized the linear layers for the query, key, and value matrices in the multi-head attention module with bias vectors, which is not required or recommended; however, to be able to load the weights correctly, we have to enable these too by setting qkv_bias to True in our implementation, too We are also using the 1024 token context length that was used by the original GPT-2 model(s)

# Define model configurations in a dictionary for compactness
model_configs = {
    "gpt2-small (124M)": {"emb_dim": 768, "n_layers": 12, "n_heads": 12},
    "gpt2-medium (355M)": {"emb_dim": 1024, "n_layers": 24, "n_heads": 16},
    "gpt2-large (774M)": {"emb_dim": 1280, "n_layers": 36, "n_heads": 20},
    "gpt2-xl (1558M)": {"emb_dim": 1600, "n_layers": 48, "n_heads": 25},
}

# Copy the base configuration and update with specific model settings
model_name = "gpt2-small (124M)"  # Example model name
NEW_CONFIG = GPT_CONFIG_124M.copy()
NEW_CONFIG.update(model_configs[model_name])
NEW_CONFIG.update({"ctx_len": 1024, "qkv_bias": True})

gpt = GPTModel(NEW_CONFIG)
gpt.eval();

The next task is to assign the OpenAI weights to the corresponding weight tensors in our GPTModel instance

def assign(left, right):
    if left.shape != right.shape:
        raise ValueError(f"Shape mismatch. Left: {left.shape}, Right: {right.shape}")
    return torch.nn.Parameter(torch.tensor(right))

import numpy as np

def load_weights_into_gpt(gpt, params):
    gpt.pos_emb.weight = assign(gpt.pos_emb.weight, params['wpe'])
    gpt.tok_emb.weight = assign(gpt.tok_emb.weight, params['wte'])
    
    for b in range(len(params["blocks"])):
        q_w, k_w, v_w = np.split(
            (params["blocks"][b]["attn"]["c_attn"])["w"], 3, axis=-1)
        gpt.trf_blocks[b].att.W_query.weight = assign(
            gpt.trf_blocks[b].att.W_query.weight, q_w.T)
        gpt.trf_blocks[b].att.W_key.weight = assign(
            gpt.trf_blocks[b].att.W_key.weight, k_w.T)
        gpt.trf_blocks[b].att.W_value.weight = assign(
            gpt.trf_blocks[b].att.W_value.weight, v_w.T)

        q_b, k_b, v_b = np.split(
            (params["blocks"][b]["attn"]["c_attn"])["b"], 3, axis=-1)
        gpt.trf_blocks[b].att.W_query.bias = assign(
            gpt.trf_blocks[b].att.W_query.bias, q_b)
        gpt.trf_blocks[b].att.W_key.bias = assign(
            gpt.trf_blocks[b].att.W_key.bias, k_b)
        gpt.trf_blocks[b].att.W_value.bias = assign(
            gpt.trf_blocks[b].att.W_value.bias, v_b)

        gpt.trf_blocks[b].att.out_proj.weight = assign(
            gpt.trf_blocks[b].att.out_proj.weight, 
            params["blocks"][b]["attn"]["c_proj"]["w"].T)
        gpt.trf_blocks[b].att.out_proj.bias = assign(
            gpt.trf_blocks[b].att.out_proj.bias, 
            params["blocks"][b]["attn"]["c_proj"]["b"])

        gpt.trf_blocks[b].ff.layers[0].weight = assign(
            gpt.trf_blocks[b].ff.layers[0].weight, 
            params["blocks"][b]["mlp"]["c_fc"]["w"].T)
        gpt.trf_blocks[b].ff.layers[0].bias = assign(
            gpt.trf_blocks[b].ff.layers[0].bias, 
            params["blocks"][b]["mlp"]["c_fc"]["b"])
        gpt.trf_blocks[b].ff.layers[2].weight = assign(
            gpt.trf_blocks[b].ff.layers[2].weight, 
            params["blocks"][b]["mlp"]["c_proj"]["w"].T)
        gpt.trf_blocks[b].ff.layers[2].bias = assign(
            gpt.trf_blocks[b].ff.layers[2].bias, 
            params["blocks"][b]["mlp"]["c_proj"]["b"])

        gpt.trf_blocks[b].norm1.scale = assign(
            gpt.trf_blocks[b].norm1.scale, 
            params["blocks"][b]["ln_1"]["g"])
        gpt.trf_blocks[b].norm1.shift = assign(
            gpt.trf_blocks[b].norm1.shift, 
            params["blocks"][b]["ln_1"]["b"])
        gpt.trf_blocks[b].norm2.scale = assign(
            gpt.trf_blocks[b].norm2.scale, 
            params["blocks"][b]["ln_2"]["g"])
        gpt.trf_blocks[b].norm2.shift = assign(
            gpt.trf_blocks[b].norm2.shift, 
            params["blocks"][b]["ln_2"]["b"])

    gpt.final_norm.scale = assign(gpt.final_norm.scale, params["g"])
    gpt.final_norm.shift = assign(gpt.final_norm.shift, params["b"])
    gpt.out_head.weight = assign(gpt.out_head.weight, params["wte"])
    
    
load_weights_into_gpt(gpt, params)
gpt.to(device)

If the model is loaded correctly, we can use it to generate new text using our previous generate function:

torch.manual_seed(123)

token_ids = generate(
    model=gpt,
    idx=text_to_token_ids("Every effort moves you", tokenizer),
    max_new_tokens=25,
    context_size=NEW_CONFIG["ctx_len"],
    top_k=50,
    temperature=1.5
)

print("Output text:\n", token_ids_to_text(token_ids, tokenizer))

Output text:
 Every effort moves you toward finding an ideal new way to practice something!

What makes us want to be on top of that?

41.10.6. Your turn! 🚀

tbd.

41.10.7. Acknowledgments

Thanks to Sebastian Raschka for creating the open-source course Build a Large Language Model (From Scratch). It inspires the majority of the content in this chapter.